Part 6: 音の立ち上がりとスペクトラル・フラックス

原文: Onset Detection Part 6: Onsets & Spectral Flux

今までの投稿では音の立ち上がり/ビート検出について科学的な観点から説明してきた。この目的を果たすのにもっとうまくやれたり、あまりうまくやれなかったりするスキーマはもっとたくさん存在する。しかし、ある方法が謎なほどシンプルでほかのもっと精緻なアルゴリズムよりうまく動いたので、私はこのアルゴリズムを選んだ。それがスペクトラル・フラックスまたはスペクトラルディファレンス解析というものであり、この記事ではこのアルゴリズムについて洞察しよう。

音の立ち上がり検出というテーマについての最高の論文の 1 つは Bello その他によるものだ。ここで読める。ここではこの論文で言及された概念のいくつかについて説明し、何個かの画像を転用させてもらう。

最初に音の立ち上がりとは何だ？下記を見てほしい:

(TODO: 画像)

一番上には 1 つの音のサンプルの振幅、つまり波形が見られる。音の立ち上がりは 1 つの音を演奏するときに最初に起こることであり、そのあと振幅が最大値に達するまでアタックが起こり、そのあとディケイが続く。今回はあまり関係ないのでトランジェントについては定義するのは差し控えておく。

私たちが処理したい音声信号はもちろん 1 つの音よりほんの少し複雑だ。ギターやバイオリン、ボーカルのように調性のある楽器、調性のないドラムを含む多声的な音楽から音の立ち上がりを検出したいのだ。2, 3 個前の記事で見た周波数チャートから分かるように、調性のある楽器は周波数の範囲 (たいていは 70Hz～4000Hz) において重なり合っている。それゆえ完璧な音の立ち上がり検出は不可能だが、近似的な見積もりを得るために試行することは可能だ。

このトピックに関する複数の論文を読んでみた知識から総合すると、音の立ち上がり検出はいつも同じスキーマに従っている。最初に音声信号を読み込み、次にそれを音の立ち上がり検出用の関数に変換し (元々の音声信号になんらかのやり方で対応しているもう一つの float 配列に過ぎない)、最後にこの検出用の関数からピークを選び出しそれを音の立ち上がり/ビートとする。最初の段階についてはすでに説明し非常に簡単であることが分かった。処理の第二の段階はたいていかなり複雑で、なんらかの魔法を使い音声信号をもう 1 つのよりシンプルな、圧縮された 1 次元の関数に変換する。最後の段階についてはほとんどの文献で詳細まで論じられていない。しかし、プロトタイプを作りながら気づいたのは、この段階がおそらくはもっとも重要で、音の立ち上がり検出の関数による計算よりも重要かもしれないということだった。今後の記事ではピーク検出にも集中するが、今は音の立ち上がり検出の関数に専念しよう。

下記は音の立ち上がり検出の一般的な過程を説明した小さな表だ。再び Bello et al から拝借した。

(TODO: 画像)

処理の前段階としてたとえばダイナミックレンジ圧縮 (dynamic range compression, DRC) を行う。これはすべてを同じ音量まで高めることであり、今日の音楽のミックスのほとんどすべてで利用されているつまらない習慣だ。しかし、DRC をつまらなく感じたとしても、それはいくつかの音の立ち上がり検出の関数にとっては有益である。今回は DRC から恩恵を受けるような関数は使わないので、処理の前段階については気にしないことにする。

縮小の段階は音の立ち上がり検出の関数を作ることに等しい。この段階におけるゴールは、音楽信号の構造について圧縮された概観を取得することだ。音の立ち上がり検出の関数は、音楽的なイベントを補足し、音声信号のそのままの波形で試すのより簡単に音の立ち上がりを検出できるべきだ。音の立ち上がり検出の関数の出力は、連続する時間の範囲の中に音楽的なイベントが存在するか不在かを示す値である。どうやって再生のためにサンプルを読み込んだかを思い出してほしい。イテレーションの中で 1024 個ずつサンプルを読み込んだ。このようなサンプル幅に対して音の立ち上がり検出の関数は値を出力する。44100Hz でサンプルされた 1 秒の音楽で、時間の範囲に 1024 個のサンプルを用いるなら、音声信号の構造をモデル化しただいたい 43 個 (44100/1024) の値が取得されるだろう。偶然にも 1024 個のサンプル幅なら、FFT クラスで処理することができる。要約すると: 音の立ち上がり検出の関数による値の生成とは、連続したサンプル幅ごとの値を計算することであり、それはピーク検出を行うためのすばらしい曲線をもたらすはずだ。

さて、前回の記事で FFT については紹介したので、音の立ち上がり検出の関数を生成するために使ってみよう。これをやる動機はなんだろう？下記の “A Perfect Circle” の “Judith” からの抜粋を聴き、下記の画像を見てみてほしい:

(TODO: 音声ファイル)

(TODO: 画像)

画像には連続する 1024 サンプル幅の音声信号スペクトラムが描かれている。縦に見たピクセルの 1 カラム 1 カラムは 1 つのスペクトラムに対応している。カラムの中のそれぞれのピクセルは周波数ビンを表している。色によってその周波数ビンがスペクトラムが抽出されたサンプル幅中の音声信号にどのくらい貢献しているかが分かる。色の値の範囲は青から赤を経過して白までであり、この順に貢献が強くなる。参照用に y 軸には周波数のラベル、x 軸には時間のラベルをつけてある。そしてなんとビートが見てとれるではないか！気ままにペイントで矢印のマークをつけてみた。ビートは 5000Hz から 16000Hz あたりの高い周波数帯にしか見られない。これらはハイハットが叩かれるタイミングに対応している。ハイハットを叩くといわゆるホワイトノイズ、周波数スペクトラムのすべてまたがる音が出る。他の楽器に比べるとハイハットは叩くときに非常に強いエネルギーを持っている。これもスペクトラムのプロットの中にはっきりと確認することができる。

さて、このスペクトラムのプロットを処理するにしても、元の波形を処理しようとするのに比べてそんなに簡単ではない。比較のために、下記に同じ曲の抜粋の波形を示す：

(TODO: 画像)

波形でもハイハットが打たれたところは分かる。それではフーリエ変換という方法を経由する利点はなんだろう？それは特定の周波数に焦点を当てることができるということだ。たとえば、ハイハットまたはクラッシュまたはライドのビートだけを検出することに興味があるのなら、非常に高い周波数だけに注目すればよい。これらの楽器はそのような周波数にのみ存在感のある音を残すからだ。振幅だけではこのようなことはできない。楽器にも同じことが言えて、キックドラムやベースなら低い周波数だけに注目すればよい。複数の周波数帯のスペクトラムを別々に調査するのは、複数帯音の立ち上がり検出 (multi-band onset detection) と呼ばれている。このキーワードが気になったらググってみるとよい。

このようになぜ周波数領域で音の立ち上がり検出を行うべきなのかは分かったが、スペクトラムのプロットに含まれるすべての情報を圧縮して、ピーク検出をしやすい管理可能な 1 次元配列にする方法についてはまだ分かっていない。ここで新しい我々のベストフレンドであるスペクトラル・ディファレンスまたはスペクトラル・フラックスを紹介しよう。コンセプトは信じられないぐらいにシンプルだ: スペクトラムのそれぞれに対して現在のスペクトラムより 1 つ前の同じサンプル幅のスペクトラムとの差を計算する。それだけ。これによって得られるのは現在のスペクトラムのビン値と、1 つ前のスペクトラムのビン値との絶対値としての差を表す 1 つの数だ。これがそのいい感じの数式だ (数式を書くために wordpress の latex プラグインを使うことになった):

math SF(k) =\displaystyle \sum_{i=0}^{n-1} s(k,i) – s(k-1,i)

SF(k) は k 番目のスペクトラムについてのスペクトラル・フラックスを表す。s(k,i) は k 番目のスペクトラム i 番目のビンの値を示し、s(k-1,i) は k の前のスペクトラムについて i 番目のビンを表す。現在のスペクトラムのビンから、前のスペクトラムの対応するそれぞれのビンを引き、最後の値にたどりつくまでその差を足していけば、それがスペクトラム k のスペクトラム・フラックスだ。

ある mp3 ファイルのスペクトラル・フラックスを計算して可視化する小さなプログラムを書いてみよう:

public class SpectralFlux 
{
   public static final String FILE = "samples/judith.mp3";	
	
   public static void main( String[] argv ) throws Exception
   {
      MP3Decoder decoder = new MP3Decoder( new FileInputStream( FILE  ) );							
      FFT fft = new FFT( 1024, 44100 );
      float[] samples = new float[1024];
      float[] spectrum = new float[1024 / 2 + 1];
      float[] lastSpectrum = new float[1024 / 2 + 1];
      List spectralFlux = new ArrayList( );
		
      while( decoder.readSamples( samples ) > 0 )
      {			
         fft.forward( samples );
         System.arraycopy( spectrum, 0, lastSpectrum, 0, spectrum.length ); 
         System.arraycopy( fft.getSpectrum(), 0, spectrum, 0, spectrum.length );
			
         float flux = 0;
         for( int i = 0; i < spectrum.length; i++ )			
            flux += (spectrum[i] - lastSpectrum[i]);			
         spectralFlux.add( flux );					
      }		
				
      Plot plot = new Plot( "Spectral Flux", 1024, 512 );
      plot.plot( spectralFlux, 1, Color.red );		
      new PlaybackVisualizer( plot, 1024, new MP3Decoder( new FileInputStream( FILE ) ) );
   }
}

まず mp3 ファイルからサンプルを読み込むデコーダーのインスタンスを生成する。また、FFT のオブジェクトも生成し、1024 個のサンプル幅と 44100Hz のサンプリングレートを設定する。次にデコーダーから読み込むサンプルを保存するための float 配列を作成する。幅の数には 1024 個のサンプルを使う。次の 2 行では現在のスペクトラムと 1 つ前のスペクトラムを保存するための補助的な float 配列を生成する。最後にそれぞれのサンプル幅に対するスペクトラム・フラックスを書き込むための場所も必要であり、ここでは ArrayList がその役割を果たす。

次のループの中ではスペクトラム・フラックスを計算する汚い仕事を行っている。最初にデコーダーから次の 1024 サンプルを読み込む。それが成功したら fft.forward(samples) の呼び出しによりこのサンプル幅に関するフーリエ変換とスペクトラムの計算を行う。それから直前のスペクトラムを lastSpectrum 配列にコピーし、今計算したばかりのスペクトラムを spectrum 配列へコピーする。そのあとに続くのは上記の公式の実装だ。それぞれのビンについて現在のスペクトラムのビンから直前のスペクトラムのビンの値を引き、flux という名前の合計を保持する値に足す。ループが終わると flux には現在のスペクトラムのスペクトラル・フラックスが含まれている。この値は spectralFlux ArrayList に追加され、続けて次のサンプル幅のデコード処理が行われる。これをデコーダーから読み込んだそれぞれのサンプル幅に対して繰り返す。ループが終わると spectralFlux には読み込んだそれぞれのサンプル幅に対するスペクトラル・フラックスが含まれる。最後の 3 行でプロットを作成し、結果を可視化している。注意: PlaybackVisualizer という名前の小さなヘルパークラスを作成した。このクラスはプロットと、ピクセル毎のサンプルの数と、デコーダーを引数に取り、デコーダーから受け取った音声を再生しつつ、再生時間に合わせてプロットの中にマーカーを設定してくれる。何も複雑なことはなく、やり方は前の記事で見た。下記は上でもすでに利用した “Judith” という曲の出力結果だ:

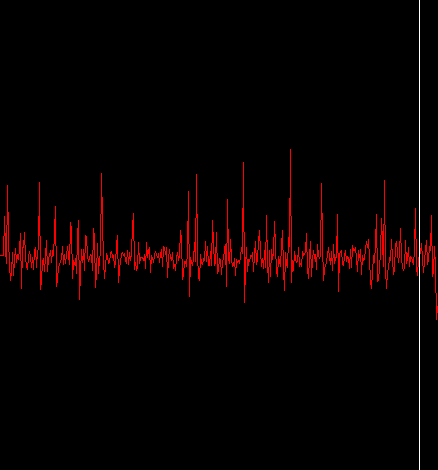
バンザイ！またピークが確認できた。今度はハイハットだけでなくスネアやキックドラムに対応している。これは、完全なスペクトラムを使うとスペクトラル・フラックスの値がもっともエネルギーのある楽器、この場合はハイハット・スネア・キックドラムに支配されるからだ。今やったことの復習をしよう。上記の元々のスペクトラムをとってきてハイハットのヒットをマークしてみた。コードがしているのは本質的には 2 つの連続したスペクトラムのビンの差を合計することだ。現在のスペクトラムが前のスペクトラムより全体として大きいエネルギーを持っているとき、スペクトラル・フラックスは上昇する。現在のスペクトラムが前のスペクトラムより小さなエネルギーしか持っていないときにはスペクトラル・フラックスは下降する。よって 2 次元のスペクトラムのプロットをピーク検出を実行できる 1 次元の機能にマッピングできたわけだ。どんな形にせよ。

ピーク検出を行う前にスペクトラル・フラックス関数を少しだけ整理しなければならない。スペクトラル・フラックスの値が負の数のとき無視するようにすることからはじめよう。降下するスペクトラル・フラックスではなく、上昇するスペクトラル・フラックスにだけ興味があるからだ。負のスペクトラル・フラックスの値を無視するプロセスは「整流」(rectifying) と呼ばれる。これがスペクトラル・フラックスを計算するループを修正したものだ。

float flux = 0;
   for( int i = 0; i < spectrum.length; i++ )			
   {
      float value = (spectrum[i] - lastSpectrum[i]);			
      flux += value < 0? 0: value;
   }
   spectralFlux.add( flux );

そしてこれに対応する出力がこれ:

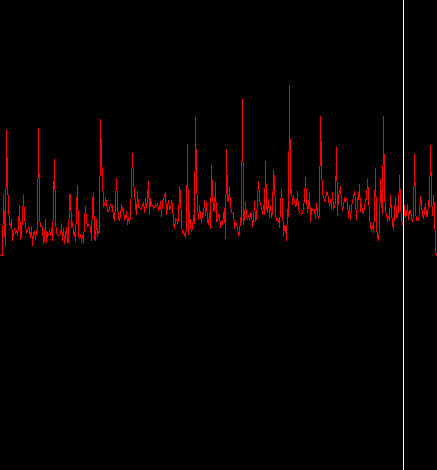
ちょっとだけ良くなった。スペクトラル・フラックスを修正したのでピーク関数のためにしきい値を計算するのが楽になるだろう。

もう 1 つ整理するプロセスとしていわゆるハミング窓を使う。このハミング窓というのはフーリエ変換の計算を行う前にサンプルに適用される。これはサンプルをちょっとよくする平滑剤のような役割を果たす。FFT クラスはハミング窓による平滑化を有効にする機能を持っている。

fft.window(FFT.HAMMING);

やるべきことはすべて終わった。これが結果だ:

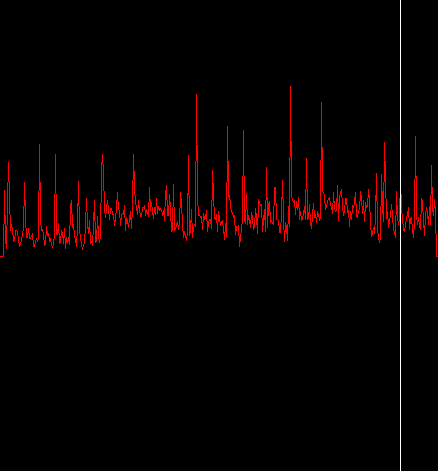
そんなに大きな違いはないが最初の 4 つのヒットが少し均質化 (TODO) されたのと、サンプルの最後の 1 つのヒットが除去されたのが分かる。他の曲ではハミング窓はスペクトラル・フラックスに対してより大きな効果を持つことがあるが、使うかどうかはあなた次第だ。大幅にパフォーマンスを犠牲にしてしまうようなことは起こらない。

これをもってこの記事を締めくくろうと思う。サンプルからはじめて、スペクトラムを計算し、ゆくゆくはピーク、すなわち音声信号における音の立ち上がりを検出するために使う 1 次元配列を計算する方法を見てきた。上記の画像から、容易に検出できそうなたくさんのピークがすでに分かると思う。次の記事では 1 ステップ進んでさまざまな周波数帯のスペクトラル・フラックスを計算する。これによりスペクトラム全体で一番大きな音量の楽器にフォーカスするのではなく、さまざまな楽器を抽出できればよいと思う。また、ホッピングと呼ばれるテクニックを利用し、重なり合わないサンプル幅ではなく、重なり合う連続したサンプル幅でのスペクトラム・フラックスを計算してみる。この結果としてスペクトラル・フラックスの機能がもう少し平滑になるだろう。それだけやれば最終的な音の立ち上がり時間を教えてくれるシンプルだが効果的なピーク検出器を作る準備は完了だ。

いつも通り、すべてのソースコードは http://code.google.com/p/audio-analysis/ で見つかる。以上。